|
A beam AB whose weigh is M and is located at an angle of α from the wall and is hinged at point A to the wall, a cable is connected to the wall and the beam end at point B as shown in the figure. Find the direction and the value of the force acting on hinge A and the tension in the cable CB.
From the free body diagram, we can write the equilibrium equations in the x and y directions:
| x direction: |
Fx − T sinθ = 0 |
(1) |
| y direction: |
Fy + T cosθ − mg − M g = 0 |
(2) |
Another condition that should be fulfilled is that the sum of the moments at the hinge A is ΣMA = 0
If α + θ is not 90 degree then we have to calculate the projection of T that is perpendicular to the beam which is T sin(α + θ)
Moments at A:
| m g L sinα + M g sinα L / 2 − T sin(α + θ) L = 0 |
(3) |
from eq. (3) we can find the value of T.
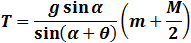 | (4) |
| Substitute eq. (4) into eq. (1) and (2) we get the forces Fx and Fy : |
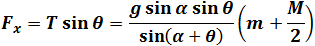 | (5) |
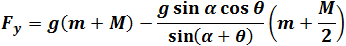 | (6) |
Once we found Fx and Fy we can find the reaction force F and the angle of the reaction γ on hinge A.
If α + θ = 90 degree then T Fx and Fy are:
The weight of a uniform horizontal beam is 10kgf a weight of m = 500kgf is hanged on point B . A cable holds the end of the beam to the wall at an angle of 60 degree. Find the reaction force on hinge A and its direction.
(run example).
Because α + θ = 150 degree we have to use eq. (4) (5) and (6).
Given the weight W which is equal to m g = W
| Tension is: |
T = sin 90 (500 + 10 / 2)/cos(90 + 60 − 90) = 1010 kgf |
| Fx is: |
Fx = sin90 sin60 (500 + 10 / 2) / sin150 = 874.7 kgf |
| Fy is: |
Fy = 510 − sin90 cos60 (500 + 10 / 2) / sin150 = 5 kgf |
| γ is: |
γ = arctan (874.7 / 5) = 89.7 degree |
|