|
The Game of Life was invented by the British mathematician John Horton Conway in
1970. The game has an unlimited number of initial patterns of squares and they
evolves by strict rules into surprising shapes, each generation is a function of
the previous generation. The rules are applied every generation on each cell. The
game was investigated by many scholars as a simulation tool.
A random start pattern usually will stabilize. Conway offered a prize for any
example of pattern that grows forever. Such a pattern was found shortly after.
|
| The rules of the game |
|---|
| 1 |
Any cell can have from 0 up to 8 neighbors maximum. |
| 2 |
Any live cell with fewer than two live neighbours dies, as if caused by under-population. |
| 3 |
Any live cell with two or three live neighbours lives on to the next generation. |
| 4 |
Any live cell with more than three live neighbours dies, as if by overcrowding. |
| 5 |
Any dead cell with exactly three live neighbours becomes a live cell, as if by reproduction. |
| Example: The numbers inside the squares indicates number of neighbours. |
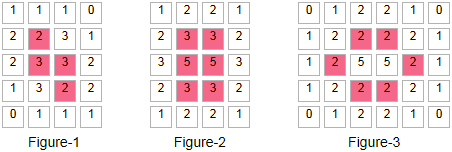 |
| The shape at figure-3 is a still one and is not changed by the generation change. |
| NOTES: |
|
To demonstrate a real game the grid should be an infinite size. In order to simplify the
code written we has limited the size of the grid boundary to 16 celles, this will highly reduce the boundary distortion. It is possible to choose a
greater gride size to explore the behavior of various shapes.
|