Tangent lines from a point to circle Print intersection of two planes calculator ▲
Circles form:   (x-a)2 + (y-b)2 = r2 ( x - )2 + ( y - )2 = 2
Circles form:   x2 + y2 + Ax + By + C = 0 x2 + y2 + x + y + = 0
Point outside the circle:     input (x, y): ( , )
Circle equation:
Tangent line 1 Equation:
Tangency point:
Tangent line 2 Equation:
Tangency point:
Distance from point to circle center:
Line connecting circle center to the point Line equation:
Line angle:
Degree
x axis intercept:
y axis intercept:
     
Circle equations summary Line Geometry Example 1 Example 2
Tangent lines between circle and point Print tangent lines between circle and point summary ▲
Tangent points from a point
(xp , yp) on a circle.
Scheme of tangent line to circle
Example: Find the tangent points on the circle (x − 2)2 + (y + 5)2 = 9   from point (7 , 1).
In this case:    a = 2    b = − 5    r = 3
The value of the square root is:
x1 = 4.87         x2 = 0.61
y1 = − 5.89         y2 = − 2.34
So first tangency point is:
(4.87,-5.89) and the second point is the other points: (0.61,-2.34)
Now we can check if the tangent point that we found is on the circle:
(4.866-2)2 + (-5.888 + 5)2 =
2.8662 + (-.888)2 = 9
Note: we used higher precision of the point coordinate otherwise we would get slightly different value then 9.
nomenclature:
D − Distance from point to circle center
d − Distance from point to tangent point
θ − Angle between the two tangent lines
x1,2Tangent points x coordinates
y1,2Tangent points y coordinates
xiline connecting point to
circle center x intercept
yiline connecting point to
circle center y intercept
The distance between the point (xp , yp) and the tangent point (1) is:
The angle between the two tangent lines   θ   is:
Note: in the equations above x1 can be replaced by x2.
Circle form: x2 + y2 = r2
Line connecting point (xp , yp) with circle center
equation:
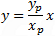x intercept: xi = 0
y intercept: yi = 0
Circle form: (x − a)2 + (y − b)2 = r2
Line connecting point (xp , yp) with circle center
equation:
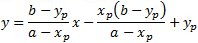x intercept:
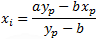y intercept:
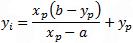Circle form: x2 + y2 + Ax + By + C = 0
Line connecting point (xp , yp) with circle center
equation:
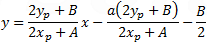x intercept:
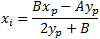y intercept:
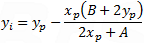If two points (x1 , y1)   and (x2 , y2) on the circle are given then the intersection point (xp , yp ) created by the tangents lines is:
Where: and
Example 1 - Circle tangent lines Print example circle tangent lines ▲
Find the equations of the line tangent to the circle given by:  x2 + y2 + 2x − 4y = 0  at the point  P(1 , 3).
Tangent line
The incline of a line tangent to the circle can be found by implicit derivation of the equation of the circle related to x (derivation dx / dy)
If the equation of the circle is:
Ax2 + Ay2 + Bx + Cy + D = 0
Then the implicit derivation is:
2Ax+2Ay dy/dx+B+C dy/dx=0
dy/dx=(-2Ax-B)/(2Ay+C)
dy/dx=m=(-2∙1∙1-2)/(2∙1∙3-4)=-2
The slope of the tangent line can be expressed by the points (x , y) and P as the tangent of  θ  or  m  as:
m=(y-3)/(x-1) (tangent of the line)
y − 3 = mx − m mx − y + 3 − = 0
And the equation of the tangent line is:      2x + y − 5 = 0
Example 2 - Circle tangent lines Print example circle tangent lines ▲
Find the equations of the tangent lines to the circle given by the equation:  x2 + y2 + 4x + 6y − 21 = 0  from the point  P(−4 , 5).
Example 2 - general tangency of two lines and a circle
A simple way to find the points S and Q is by applying geometric methods.
The distance from the point to the circle center is:
(PO) ̅=√((x_p-x_c )^2+(y_p-y_c )^2 )
Example 2 - two tangents lines
First, we shell find the center and the radius of the circle, by the procedure for completing the square:
(x^2+4x)+(y^2+6y)-21=0
(x+2)^2-4+(y+3)^2-9-21=0
(x+2)^2+(y+3)^2=34
We can see that the center of the circle is at  (−2 , −3)  and the radius is equal to:  √34.
Since point  Q  is common to the line and the circle, its  x  and  y  coordinates are the same and we have to solve the set of equations:
Ax+By+C=0 (x-c)^2+(y-k)^2=r^2
From the line equation after eliminating y we get y=(-Ax-C)/B substitute y into the circle equation.
(x-c)^2+(-A/B x-(C+Bk)/B)^2=r^2
x^2-2cx+c^2-A^2/B^2 x^2-2A(C+Bk)/B x-(4A^2)/B^2 (C+Bk)^2-r^2=0
x^2 (1-A^2/B^2 )-x(2c-2A(C+Bk)/B)+c^2-(4A^2)/B^2 (C+Bk)^2-r^2=0
this is a quadratic equation for  x: