Two circles track calculator Print two circles track calculator ▲
Circles of the form:     (x-a)2 + (y-b)2 = r2
Circle 1: ( x - )2 + ( y - )2 = 2
x2 + y2 + x + y + = 0
Circle 2: ( x - )2 + ( y - )2 = 2
x2 + y2 + x + y + = 0
Circles of the form:     x2 + y2 + Ax + By + C = 0


First circle radius (R)
Second circle radius (r)
Distance of circles centers (d)
Angle (θ)
Angle (α)
Length (h)
Track length (L)
         Degree   Radian       
Angular velocity of pulley R
Angular velocity of pulley r
Relative circle’s locations summary Track calculation example
Two circles track Print two circles track summary ▲
Two circles track
Given two radii and distance between circles centers (R, r, d), case:   R > r
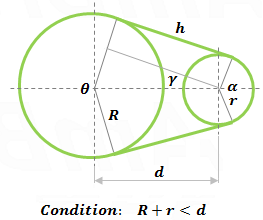
Circles track
θ + α = 2π
If r > R then θ is less then 180 ̊
and γ is negative
θ = 2π − α
When R = r then L reduces to:
L = 2d + 2πR
Note: we used in all the equations the relation   R > r
Angle γ is: 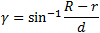Axis angle (R > r)
Angles between the line connecting the two tangent points of radii R and r are θ and α and the axis:
Angles
Angles
Arc lengths between the two tangent points of radii R and r are:
Arc lengths
Arc lengths
Tangent line length
Tangent line length
And the total track length L is:
L = 2h + Rθ + rα = 2h + Rθ + r(2π − θ)
Total track length
Total track length
If the circles are given by:
(x − a)2 + (y − b)2 = R2
(x − c)2 + (y − d)2 = r2
The distance between centers is: Distance between circles centers
Other parameters are the same:
If the circles are given by:
x2 + y2 + Ax + By + C = 0
x2 + y2 + Dx + Ey + F = 0
The distance between centers is: Distance between circles centers
Circles radii
Other parameters are the same as before.
Relative conditions for two circles locations Print relative conditions for two circles locations summary ▲
Drawing Condition
Circle in circle
Circles equations: (x − a)2 + (y − b)2 = r02
(x − c)2 + (y − d)2 = r12
Distance between circles centers: Distance between circles centers
d < |r0 − r1|
Circle in circle
Inner tangency
d = |r0 − r1|
Circle in circle
Outer tangency
d = r0 + r1
Circle in circle
Intersecting circles
|r0 − r1| < d < r0 + r1
Circle in circle
Two separate circles
d > r0 + r1
Track example Print relative conditions for two circles locations summary ▲
Circular track example Two pulleys of  20 cm  and  10 cm  radii are connected by a belt. The distance between the centers of the pulleys is  0.5 m.  Find the length of the belt and the angular velocity of the big pulley if the small pulley is rotating at a rate of  100 rpm.
Circular track example
Figure - 1
 From figure 1 we see that triangles  ACD  is similar to triangle  ABE (all the angles are the same).
We have the relations:
sin⁡γ=r/b=R/(a+b)
Now we can find the value of  b  that is:
b=ra/(R-r)=(0.04∙0.7)/(0.1-0.04)=0.466 m
Calculate the angle  γ  by the equation: γ=sin^(-1)⁡〖r/b〗=sin^(-1)⁡〖0.08/0.466〗=9.9 deg
The value of  h  can be calculated by Pythagoras theorem:
h=√(a^2-(R-r)^2 )=√(〖0.5〗^2-(0.2-0.08)^2 )=0.485m
Angle ω is: ω = 90 − γ = 90 − 11.5 = 78.5 deg
Track arc length of the big pulley is: L_R=R2(180-ω)=0.2∙2 ((180-78.5))/180 π=0.71 m
Track arc length of the small pulley is: L_r=r2ω=0.1∙2∙78.5/180 π=0.27 m
The length of the belt is: L = LR + Lr + 2h = 0.71 + 0.27 + 2 * 0.485 = 1.95 m
The circumference of the big and the small pulleys are: CR = 2 π R Cr = 2 π r
When the small pulley is performing 1 rotation the big pulley will make  r / R  rotations.
The angular velocity of the big pulley is: V_R=r/R V_r=0.1/0.2 100=50   rpm
And the angular velocity in  rad / s  is: ω_R=(50∙2π)/60=5.24   rad / s