Intersection of 3 planes Print intersection of 3 planes calculator ▲
Plane 1: x + y + z + = 0
Plane 2: x + y + z + = 0
Plane 3: x + y + z + = 0
Plane defined
by 3 points:		  xa   ya   za 
 xb   yb   zb 
 xc   yc   zc 
            
Intersection type:
Intersection coordinate:
det + rank:
NOTES:
Intersection line 1 equation:
 
 
 
Intersection line 2 equation:
 
 
 
Intersection line 3 equation:
 
 
 
n1 x n2         |             Angle
n1 x n3         |             Angle
n2 x n3         |             Angle
Solved problems: Intersection of 3 planes Ex2 Ex3 Ex4 Three parallel planes
Intersection of 3 planes summary Print intersection of 3 planes summary ▲
Three planes intersection.
Plane 1:     A1 x + B1 y + C1 z = D1
Plane 2:     A2 x + B2 y + C2 z = D2
Plane 3:     A3 x + B3 y + C3 z = D3
Normal vectors to planes are:
n1 = iA1 + jB1 + kC1
n2 = iA2 + jB2 + kC2
n3 = iA3 + jB3 + kC3
For intersection line equation between two planes see two planes intersection.
 In order to find which type of intersection lines formed by three planes, it is required to analyse the ranks   Rc   of the coefficients matrix and the augmented matrix   Rd.
Rank:
Rank:
If vectors:    n1 × n2 = 0    then the planes are parallel (cross product).
The angle between two planes from the vectors dot product is:
Angle between two planes
Plane - P1
Plane - P2
Plane - P3
Condition for a single point of intersection is:
rank Rc = 3
rank Rd = 3
Intersection point is given by Cramer's rule:
In vector analysis:     n1 · (n2 × n3) ≠ 0             (Example 4)
Condition for one line intersection (two coincide planes) are:
rank   Rc = 2         and         Rd = 2
In vector analysis:     n2 × n3 = 0         n1 × n3 = n1 × n2 ≠ 0
Condition for one line intersection is:              (Example 3)
rank   Rc = 2         and         Rd = 2
In vector analysis:     n1 × n2 = n1 × n3 = n2 × n3 ≠ 0
Note:   n1 is the same as   −n1   but pointing to the opposite direction.
The reason for this is the fact that:     n1 × n2 = −n2 × n1
Condition for two lines intersection (two parallel planes) is:
rank   Rc = 2         and         Rd = 3
In vector analysis:     n2 × n3 = 0         n1 × n3 = n1 × n2 ≠ 0
Condition for three lines intersection is:
rank   Rc = 2         and         Rd = 3
All values of the cross product of the normal vectors to the planes are not 0 and are pointing to the same direction.
n1 × n2 = n1 × n3 = n2 × n3 ≠ 0
Condition for no intersection (three parallel planes) are:
rank   Rc = 1         and         Rd = 2
Check number of similar planes Rs:         Rs = 0        (Example 2)
In vector analysis:     n1 × n2 = n1 × n3 = n2 × n3 = 0
Condition for no intersection (three parallel planes, 2 coincides) are:
rank   Rc = 1         and         Rd = 2
Check number of similar planes Rs:         Rs = 2         (Example 2)
In vector analysis:     n1 × n2 = n1 × n3 = n2 × n3 = 0
Condition for no intersection (three coincide planes) are:
rank   Rc = 1         and         Rd = 1
In vector analysis:     n1 × n2 = n1 × n3 = n2 × n3 = 0
The cross product is equal to:
Example 1 - Intersection of 3 planes Print intersection of 3 planes example ▲
Investigate the intersection values between the three planes:Plane 1:     2x − y + z + 3 = 0
Plane 2:     2x + y + z + 2 = 0
Plane 3:     − 4x + 2y − 2z − 6 = 0
First find the rank of the coefficient matrix by upper triangularization.
Rc = 2
Rd = 2
The ranks can be found by two steps, first subtract the second row from the first row and then the second step is to subtract the fourth row from the first row multiplied by two.
If we look on the augmented matrix, we see that we have two equations with three unknowns so we can choose one value for example z = t and because B1/D1 ≠ 0 we have the solution for y the value y = 0.5 now the value of x will be from the first raw:
2x - y + z = -3
x = (y - z -3)/2
x = (0.5 -t -3)/2 = -1.25 - 0.5t
Thus is a line presented pay parameter t:
L{x,y,z}={− 1.25 − 0.5t,    0.5,    t}    same as    {− 1.25 − t,    0.5,    2t}     After multiplying both t by 2.
We could find the intersection line by vectors calculation, the planes are described by the vectors in i, j and k direction
n1 = 2i − j + k
n2 = 2i + j + k
n3 = − 4i + 2j − 2k
Now we can perform the cross product on each pair of the vectors.
L2 is equal to 0 that is because the two plans 1 and 3 are parallel.
We also see that lines L1 and L2 are pointing to the same direction    − 4i + 8k = − 2i + 4k    (vectors can be factored without changing their direction).
Now that we have the intersection line direction, we need a point on the line in order to set the line equation, because   Rd = 2   we must have the value of   y   from the Rd matrix:    y = 1/2 = 0.5
now we can choose an arbitrary value to z let say   z = 0   than   x = − 1.25t   or parametric line equation:
L{x,y,x} = {− 1.25 − 2t,    0.5,    4t}
Because   Rc = 2   and   Rd = 2   then two planes are parallel and because one cross product of the vectors are   0   the intersection looks like:
The angle between plane 1 and plane 2 is found from the dot product:     A · B = |A||B| cos θ
Example 2 - Intersection of 3 parallel planes Print intersection of 3 planes summary ▲
Given three planes by the equations:     x + 2y + z − 1 = 0       2x + 4y + 2z − 6 = 0       4x + 8y + 4z − n = 0
Determine the locations of the planes to each other in the case that   n = 4   and second time   n = 8.
The matrix of the   x y and z   coefficients after multiplying first row by 2 and subtracting from second row and then multiplying first row by 4 and subtracting from third row we get the matrix:
x y and z matrix Rank Rc = 1    we see that all the planes are parallel (1)
In order to find the number of coincides planes we have to analyse the augmented matrix with   n = 4 after dividing second row by 2 and third row by 4 and repeating the process done on the coefficient’s matrix, we get the matrix:
x y and z augmented matrix Rank Rd = 2 (2)
In the case that n = 8 we have the augmented matrix:
x y and z augmented matrix Rank Rd = 2 (3)
We can clearly see that if we get Rd = 2 we have to check for similar planes in order to find the number of coincides planes, from the centre matrix (2) we see that the first and third planes are coincides so  Rs = 2,  from the centre matrix (3) we see that all the planes are distinct   Rs = 3
Notice: If all the planes are similar then  Rd = 1  and we don't have to check for planes similarity.
Example 3- Three planes line intersection Print example of line and point plane ▲

Given the three planes    P1: 3x + 2y − 3z − 10 = 0     P2: 7x − 2y − 2z − 5 = 0
P3:   7x + 2y − 5z − 16 = 0    Show that all three planes have a common intersection line.

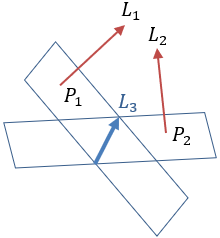
Let first analyse the intersection of two planes.
L1 and L2 are both perpendicular to planes P1 and P2 respectively, so the direction numbers of those lines are given by the attitude numbers of the planes.
In vector notation we have:
L1 = a1x + b1y + c1z     and     L2 = a2x + b2y + c2z
We can find the direction of the intersecting line L3 by cross product of vectors L1 and L2 so:   L3 = L1 × L2 = P1 × P2

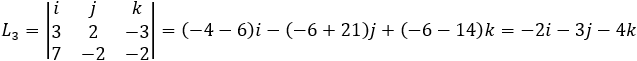
L_3=|■(i&j&k@3&2&-3@7&-2&-2)|=(-4-6)i-(-6+21)j+(-6-14)k=-2i-3j-4k

Now we can perform the same test on the pair of planes P1 and P3

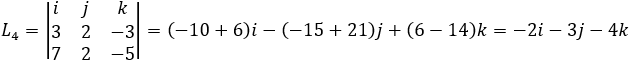
L_4=|■(i&j&k@3&2&-3@7&2&-5)|=(-10+6)i-(-15+21)j+(6-14)k=-2i-3j-4k

And the same way the pair P2 and P3

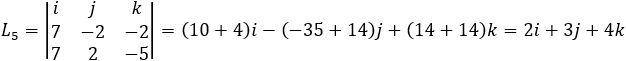
L_5=|■(i&j&k@7&-2&-2@7&2&-5)|=(10+4)i-(-35+14)j+(14+14)k=2i+3j+4k

Notice that all the intersection lines L3 , L4 and L5 has the same direction numbers values. So, they are at least parallel lines, the negative values indicate the same orientation of the line but in the opposite direction. Now we have to prove that all the lines coincide. So, we have to show that all the planes have a common line intersection. Writing the planes in set of equations we get:

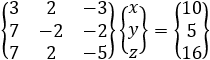
{■(3&2&-3@7&-2&-2@7&2&-5)}{■(x@y@z)}={■(10@5@16)}

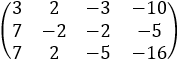The augmented matrix is (■(3&2&-3@7&-2&-2@7&2&-5) ■(-10@-5@-16))
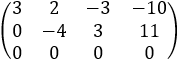After few steps on the rows, we get: (■(3&2&-3@0&-4&3@0&0&0) ■(-10@11@0))

we can see that the rank of the augmented triangular matrix Rd and the coefficients matrix Rc are:     rank = Rc = Rd = 2   This case is described in the table. This means that we have a set of three unknowns and only two equations. So, we can solve this case by setting the value of   y = t.  

Then     −4t + 3z = 11     and     z = 4t/3 − 11/3     and     x = 2t/3 − 1/3

$$ x = {2t \over 3} - {1 \over 3}$$ $$ y = t$$ $$ z = {4t \over 3} - {11 \over 3}$$

These values represent a single line that intersects all the three planes. By inserting any value for t we can find points along this line for example.

t = 0 (-1/3 , 0 , -11/3)
t = 1 (1/3 , 1 , -7/3)
Example 4- Three planes point intersection Print example of intersection of 3 planes ▲
Find the intersection point of the three planes given by the equations    2x − y + 3z − 1 = 0   
3x + y − z − 2 = 0   and   x + 2y + 3z + 6 = 0.

The first step is to check if a single intersection point exists this happens when the rank of the coefficients Rc = 3 matrix and the augmented matrix R = 3 is 3, (see table).

At the intersection point the values of x, y and z are the same for the three planes, so we have 3 equations and 3 unknowns to solve.

Solving the set of equations by Cramer's rule we get: ■(2x-y+3z=1 @3x+y-z=2 @x+2y+3z=-6)
The determinant of the coefficient’s matrix is d=|■(2&-1&3@3&1&-1@1&2&3)|=35
x=|■(1&-1&3@2&1&-1@-6&2&3)|/d=35/35=1 y=|■(2&1&3@3&2&-1@1&-6&3)|/d=-70/35=-2
z=|■(2&-1&1@3&1&2@1&2&-6)|/d=-35/35=-1

And the single point of the intersection of the three planes is:   (1 , −2 , −1)